Options trading is an advanced and versatile trading strategy that offers traders numerous opportunities to grow in various market conditions. Understanding the intricacies of advanced options trading, inlllcluding options Greeks, volatility strategies, pricing models, and risk management, is essential for success.
In this comprehensive guide, we will delve into the world of advanced options trading, covering everything from the overview of advanced options trading to the strategies and the intricacies of their implementation.
As a trader who is knowledgeable about the basics of options trading, this guide will provide you with the skills and insights needed to navigate the complex world of advanced options trading effectively.
This blog covers:
- Overview of advanced options trading
- Why is options trading attractive?
- Primary Options Greeks
- Impact of Options Greeks on options pricing and on portfolio management
- Skills for implementing advanced options trading strategies
- What is Put-Call parity in Python?
- Options Pricing
- Options pricing models
- Butterfly options trading strategy example with Python
- Risk management in advanced options trading
- Resources to learn options trading
- Frequently asked questions on advanced options trading
Overview of advanced options trading
Advanced options trading ventures beyond basic buying and selling of calls and puts. It involves useful combinations of options contracts to achieve specific trading goals.
Let us now see the concepts which are required for advanced options trading.
Essentials while performing the advanced options trading
There are some essentials of advanced options trading and these are:
- Spreads: These involve buying and selling options contracts with different strike prices or expiration dates on the same underlying asset. By combining these contracts, you create a defined risk and reward profile.
- The Greeks: Options greeks are letters representing key factors affecting option prices, including Delta, Gamma, Vega, Theta, and Rho. Understanding the Greeks is crucial for analysing and managing option positions.
- Volatility: Advanced strategies often exploit volatility expectations. Some strategies benefit from high volatility, while others profit in low volatility environments. (You can learn all about in this course on advanced volatility trading.)
Strategies involved in advanced options trading
Some common advanced options trading strategies. are:
- Long Straddle and Strangle: Buying a call and put with the same expiration date and different strike prices.
- Iron Condor and Iron Butterfly: Combining a bear call spread and a bull put spread.
- Calendar Spread: Selling a near-term option and buying a longer-term option with the same strike price.
- Butterfly Spread: A limited risk, limited reward options strategy.
Also, understanding when to exercise (buy/sell) options early to capture potential benefits or avoid unwanted assignments is crucial in advanced strategies.
Moving forward, let us find out why options trading is so attractive for traders.
Why is options trading attractive?
Options trading attracts traders for several reasons.
Here's a breakdown of the appeal: ⁽¹⁾
- Potential for maximising returns: Options offer the potential for magnified returns, especially for smaller initial investments. This leverage can be attractive, but it also amplifies potential losses, which can be managed with appropriate risk management techniques.
- Flexibility: Options provide a wider range of strategies than simply buying or selling a stock. Traders can craft positions to grow their traded amount in various market conditions (bullish, bearish, neutral, or volatile). This flexibility allows for potentially higher returns compared to basic stock trading.
- Hedging existing holdings: Options can be used to hedge existing stock positions, acting as a form of insurance against price movements. By strategically buying put options, traders can limit potential losses on their owned stocks.
- Income generation: Certain option strategies, like selling covered calls, can generate returns even if the underlying stock price remains flat. This can be attractive for income-focused investors.
- Lower capital requirement: Options often require a smaller initial investment compared to buying a stock outright, allowing traders to control the same underlying asset with less capital. This can be appealing to traders with limited capital.
However, it's essential to acknowledge that options trading carries some risks as well. These risks include the potential loss of the entire investment, rapid loss of value due to time decay, and the complexity of options strategies, which may lead to unexpected outcomes.
Therefore, it's crucial for traders to thoroughly understand options trading and employ risk management strategies to protect their investments.
Primary options Greeks
The primary options Greeks are a set of five letters representing key factors that influence the price of an option. These are the essential tools for options traders to analyse and manage risk within their positions. ⁽²⁾
Here's what each Greek signifies:
Delta (Δ)
- Measures the rate of change of an option's price in relation to a $1 change in the price of the underlying asset (stock, bond, etc.).
- A call option's Delta will typically be between 0 and 1, indicating it will move in the same direction as the underlying asset, but with a smaller magnitude.
- A put option's Delta will typically be between -1 and 0, indicating it will move in the opposite direction of the underlying asset.
Gamma (Γ)
- Represents the rate of change of Delta. It tells you how much Delta itself will change as the underlying asset price moves.
- A positive Gamma indicates Delta is increasing, meaning the option's price will become more sensitive to changes in the underlying asset price.
- A negative Gamma indicates Delta is decreasing, meaning the option's price will become less sensitive to changes in the underlying asset price.
Theta (θ)
- Measures the rate of decay of an option's price due to the passage of time, also known as time decay.
- All else being equal, the closer an option gets to expiration, the lower its price (Theta is negative).
- Theta is especially important for short-term options strategies where time decay can erode profits quickly.
Vega (ν)
- Measures the sensitivity of an option's price to changes in implied volatility.
- Implied volatility reflects market expectations of future price fluctuations for the underlying asset.
- A high Vega indicates the option's price will be more sensitive to changes in implied volatility. Conversely, a low Vega indicates the price will be less affected.
Rho (ρ)
- Measures the sensitivity of an option's price to changes in interest rates.
- Generally, higher interest rates can lead to slightly lower option prices, and vice versa. However, the effect of Rho is usually smaller compared to other Greeks.
Moving forward, we will discuss in detail the impact of options Greeks on the options pricing.
Impact of options Greeks on options pricing and on portfolio management
Here, we will again see the primary options Greeks, but will discuss the impact of each on the options pricing and also on portfolio management along with an example for each. The options Greeks each have a specific influence on how an option's price reacts to changes in various market factors as well as on the portfolio management.
|
Options Greeks |
Impact on Options Pricing |
Impact on Portfolio Management |
Example |
|
Delta |
Measures the rate of change of the option price with respect to changes in the underlying asset price |
|
|
|
Gamma |
Measures the rate of change of Delta with respect to changes in the underlying asset price |
|
|
|
Theta |
Measures the rate of change of the option price with respect to changes in time |
|
|
|
Vega |
Measures the rate of change of the option price with respect to changes in volatility |
|
|
|
Rho |
Measures the rate of change of the option price with respect to changes in interest rates. |
|
|
Now we will find out the skills needed for implementing the advanced options trading strategies.
Skills for implementing advanced options trading strategies
Here are some essential skills you'll need to develop for success with advanced options trading strategies:
Technical Knowledge
- In-depth understanding of Options Greeks: Mastering Delta, Gamma, Theta, Vega, and Rho is crucial. You should be able to interpret their influence on option pricing and portfolio behaviour.
- Volatility Analysis: Being able to assess historical and implied volatility, along with factors that affect it, is essential for crafting volatility-based strategies.
- Advanced Option Pricing Models: While basic Black-Scholes might suffice for some strategies, understanding more complex models like Heston or SABR can provide a deeper understanding of option pricing dynamics, especially in volatile markets.
- Risk Management Techniques: Advanced strategies often involve managing multiple legs (buying/selling different options). Techniques like delta hedging and spread adjustments become crucial for mitigating risk.
- Portfolio Construction: The ability to combine different option strategies to achieve specific risk-reward profiles and hedge existing holdings is a valuable skill.
Analytical Skills
- Market Analysis: Advanced strategies often rely on specific market outlooks or volatility expectations. Strong analytical skills are needed to interpret market data and technical indicators to make informed decisions.
- Backtesting Strategies: The ability to test your strategies using historical data (backtesting) helps assess their potential performance and identify weaknesses before risking real capital.
- Scenario Analysis: Considering how your positions might react to different market scenarios (upward/downward moves, volatility changes) is crucial for risk management.
Trading Skills
- Discipline and Patience: Advanced strategies often involve waiting for specific market conditions to emerge. Discipline and patience are essential to avoid impulsive trades that deviate from your plan.
- Order Management: Understanding different order types (market orders, limit orders, stop-loss orders) and how to use them effectively is crucial for managing entries and exits from your positions.
- Emotional Control: The fast-paced and potentially volatile nature of options trading can trigger emotional responses. Maintaining emotional control and sticking to your trading plan is critical for success.
Additional Skills
- Coding Skills: In today’s technology driven trading domain, basic coding knowledge (Python) can be helpful for backtesting strategies, automating calculations, or using advanced option pricing models.
- Research Skills: Staying updated on new developments in options trading strategies, market trends, and relevant financial news is important for continuous learning and adaptation.
Let us now see what put-call parity means and more about the same.
What is Put-Call parity in Python?
Put-Call Parity (PCP) is a relationship between a European call option, a European put option, the underlying asset's price, the risk-free interest rate, and the time to expiration. It essentially states that the price of a call option, adjusted for the present value of the strike price, should be equal to the price of a put option plus the current stock price.
Below is a Python code to calculate Put-Call Parity and assess its validity for a given set of parameters:
- S: Current stock price
- K: Strike price
- C: Call option price
- P: Put option price
- r: Risk-free interest rate (annualised)
- T: Time to expiration (in years)
It calculates the Put-Call Parity using the formula:
C - e^(-rT) * K = P + S
The function then displays the Left-hand side (LHS) and Right-hand side (RHS) of the equation, along with the difference between them. It also checks if the difference is close to zero, indicating that Put-Call Parity approximately holds.
Here’s the Python code:
Output:
Put-Call Parity Calculation: Left-hand side (LHS): Call option price adjusted for present value of strike - -99.63523669507855 Right-hand side (RHS): Put option price + Stock price - 107 Difference between LHS and RHS: -206.63523669507856 Put-Call Parity does not hold.
A close to zero value suggests parity holds but in the output above, it shows put-call parity does not hold.
Let us move to options pricing next.
Options pricing
Options pricing involves determining the fair value of an options contract, which gives the holder the right, but not the obligation, to buy (in the case of a call option) or sell (in the case of a put option) the underlying asset at a specified price (strike price) within a specific period of time.
Below you will find the two types of option pricing techniques and the difference between them. These types are:
- Intrinsic value of an option
- Time value of an option
Intrinsic Value of an option
The intrinsic value of an option is the value that an option would have if it were exercised immediately.
Below you can see how they are calculated.
Intrinsic Value of Call Option = Current Market Price of Underlying Asset - Strike Price Intrinsic Value of Put Option = Strike Price - Current Market Price of Underlying Asset
Time Value of an option
The time value of an option is the premium that the option buyer pays for the privilege of having the option until expiration. It reflects the probability that the option will end up in-the-money by expiration.
Time Value = Option Premium - Intrinsic Value
Going forward, we will learn about the options pricing models.
Options pricing models
Options pricing models are mathematical models used to determine the fair value of options. Below you will find the different options pricing models and the key differences between each.
|
Aspect |
Derman-Kani Model |
||
|
Introduction |
Introduced in 1973 by Fischer Black and Myron Scholes |
Proposed by Emanuel Derman and Iraj Kani in 1994 |
Developed by Steven Heston in 1993 |
|
Dynamics |
Assumes constant volatility and risk-free interest rate |
Allows for stochastic volatility and stochastic interest rates |
Incorporates stochastic volatility and mean-reverting dynamics |
|
Key Features |
Closed-form solution, widely used in finance |
Captures volatility smile, more realistic representation of market conditions |
Captures volatility smile, mean-reverting volatility, flexible and realistic |
|
Model Complexity |
Relatively simple model |
More complex than Black-Scholes, but simpler than Heston |
More complex than Black-Scholes and Derman-Kani |
|
Application |
Suitable for European options on stocks with constant volatility |
Suitable for a wider range of options, including exotic options |
Widely used for pricing options on equities, indices, and currencies |
|
Limitations |
Assumes constant volatility, doesn't capture volatility smile |
Doesn't capture all market dynamics, requires calibration |
Calibration can be complex and time-consuming, computationally intensive |
|
Example |
European call option on a stock |
Options on currencies, interest rates, and commodities |
Options on equities, indices, and currencies |
Each model has its advantages and limitations, and the choice of model depends on the specific requirements of the trader or investor.
Let us now see one of the most popular advanced options’ strategies which is the butterfly strategy and its payoff diagram.
Butterfly options trading strategy example with Python
To get to the butterfly strategy’s payoff diagram you need to follow this procedure:
- Create the strategy and know what type of options you will use.
- Know which strike prices you will use per option.
- Select a price range to which you will compare each option payoff.
- Compute the strategy payoff as the sum of the payoffs of all the options used in the butterfly strategy.
- Plot the strategy payoff as per the price range.
After learning this strategy, you will be able to plot the payoff diagram of any option strategy you might want to set up.
The steps are as follows:
Output:
futures_close Expiry Date 2022-05-20 16253.25 2022-05-26 2022-05-23 16183.35 2022-05-26 2022-05-24 16104.70 2022-05-26 2022-05-25 16013.80 2022-05-26 2022-05-26 16159.05 2022-05-26
Step 2: Select the date
Output:
'The futures price on 2021-01-01 is 14053.85'
Output:
| Symbol | Expiry | Option Type | Strike Price | Open | High | Low | Close | Last | Settle Price | Number of Contracts | Turnover | Premium Turnover | Open Interest | Change in OI | Underlying | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | ||||||||||||||||
| 2021-01-01 | NIFTY | 28-01-2021 | CE | 12000 | 2017.10 | 2062.25 | 2014.0 | 2043.60 | 2042.00 | 2043.60 | 256.0 | 269606000.0 | 39206000.0 | 456225.0 | 10200.0 | 14018.5 |
| 2021-01-01 | NIFTY | 28-01-2021 | CE | 12050 | 0.00 | 0.00 | 0.0 | 609.75 | 0.00 | 2009.45 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 14018.5 |
| 2021-01-01 | NIFTY | 28-01-2021 | CE | 12100 | 1923.15 | 1936.45 | 1922.6 | 1934.75 | 1934.75 | 1960.25 | 4.0 | 4209000.0 | 579000.0 | 15750.0 | 0.0 | 14018.5 |
| 2021-01-01 | NIFTY | 28-01-2021 | CE | 12150 | 0.00 | 0.00 | 0.0 | 569.95 | 0.00 | 1911.10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 14018.5 |
| 2021-01-01 | NIFTY | 28-01-2021 | CE | 12200 | 0.00 | 0.00 | 0.0 | 1797.80 | 1799.00 | 1862.15 | 0.0 | 0.0 | 0.0 | 22575.0 | 0.0 | 14018.5 |
Step 3: Setup the Long Butterfly Strategy
Output:
| Option Type | Strike Price | position | premium | |
|---|---|---|---|---|
| 0 | CE | 14050 | -1 | 280.75 |
| 1 | PE | 14050 | -1 | 279.00 |
| 2 | CE | 14600 | 1 | 69.25 |
| 3 | PE | 13500 | 1 | 103.00 |
Step 4: Compute the Payoff for Call and Put Options
Since we have set up the long butterfly strategy, now let's compute the payoff for call and put options.
Remember, that the payoff of a long call option is given by:
Long Call Payoff=𝑀𝑎𝑥(Spot Price−Strike Price,0)−Premium
The Max function is interpreted as the following:
- If the spot price is higher than the strike price, then the long call payoff is the difference between the spot and the strike price.
- If the spot price is lower than the strike price, then the long call payoff is 0.
Can you guess how to compute the short call? It's simple, you just need to multiply the above functions by -1 to have the short-sell version of the call option payoff.
Define the call payoff function
Step 5: Compute the Payoff for the Long Butterfly Strategy
Output:
980
Output:
- 980
Then, similarly, we can define the put option payoff.
For a long put option payoff, we have the following formula and its interpretation:
Long Put Payoff = 𝑀𝑎𝑥(Strike Price−Spot Price,0)−Premium
- If the strike price is higher than the spot price, then the long put payoff is the difference between the strike and the spot price.
- If the strike price is lower than the spot price, then the long put payoff is 0.
Output:
-20
Finally, the short put payoff value:
Output:
20
Step 6: Setup the Short Butterfly Strategy
Let's take an example. Let's call the get_payoff function for a specific price and see what the value will be at expiry.
Output:
-162.5
Output:
66 15300 67 15350 68 15400 69 15450 70 15500 Name: price_range, dtype: int64
Output:
66 -162.5 67 -162.5 68 -162.5 69 -162.5 70 -162.5 Name: pnl, dtype: float64
Output:
Output:
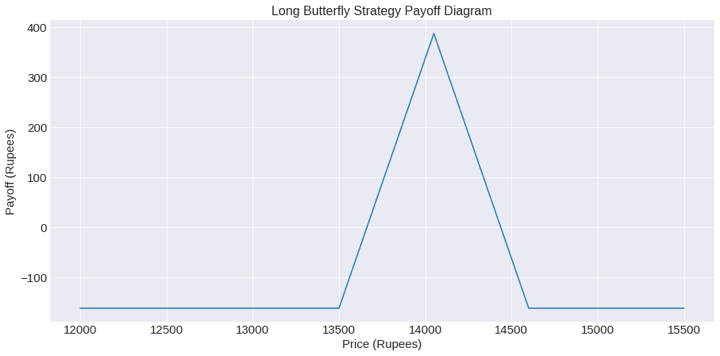
'The maximum profit is 387.5 and its corresponding futures price is 14050'
Hence, if the futures price at expiry is 14050, you can expect a maximum profit of 387.5 rupees with the strategy.
Output:
'The maximum loss is -162.5'
Step 7: Plot the Short Butterfly Strategy payoff diagram
Output:
| Option Type | Strike Price | position | premium | |
|---|---|---|---|---|
| 0 | CE | 14050 | 1 | 280.75 |
| 1 | PE | 14050 | 1 | 279.00 |
| 2 | CE | 14600 | -1 | 69.25 |
| 3 | PE | 13500 | -1 | 103.00 |
Output:
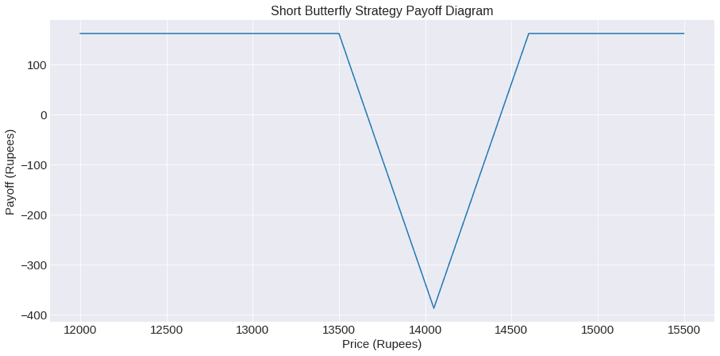
As you can see, the payoff diagram lets us visually understand when we will be getting maximum return with a long or short butterfly strategy. This code above can be used for any strategy payoff you want to obtain.
You can check the entire strategy and more on Butterfly strategy with the course on Systematic Options Trading. This course will also help you learn to backtest options trading strategies and the related concepts in detail.
It is important to note that backtesting results do not guarantee future performance. The presented strategy results are intended solely for educational purposes and should not be interpreted as investment advice. A comprehensive evaluation of the strategy across multiple parameters is necessary to assess its effectiveness.
Now, we will see how to perform risk management in advanced options trading.
Risk management in advanced options trading
Risk management is crucial in advanced options trading to protect your capital and optimise your returns.
Here are some key risk management strategies for advanced options trading:
- Position Sizing: Determine the maximum amount of capital you are willing to risk on any single trade. This ensures that you do not overexpose yourself to any one position.
- Diversification: Spread your risk by diversifying your options trades across different underlying assets, sectors, and strategies.
- Stop Loss Orders: Use stop loss orders to limit potential losses on options positions. Set stop loss levels based on your risk tolerance and the volatility of the underlying asset.
- Hedging: Hedge your options positions using strategies such as buying protective puts or selling covered calls to offset potential losses.
- Volatility Management: Be aware of the impact of volatility on options prices and adjust your positions accordingly. Consider using strategies that benefit from changes in volatility, such as straddles or strangles.
- Risk-reward Ratio: Maintain a favourable risk-reward ratio on your options trades. Aim for trades where the potential reward outweighs the potential risk by a significant margin.
- Regular Monitoring: Monitor your options positions regularly and be prepared to adjust or close them if market conditions change or your trading thesis no longer holds.
- Risk Analysis Tools: Use risk analysis tools provided by your broker or third-party software to assess the potential risks and rewards of your options trades before entering into them.
- Position Adjustment: Have a plan in place for adjusting or closing options positions that are not performing as expected. This could involve rolling positions forward, adjusting strike prices, or closing out losing positions to limit losses.
- Continuous Learning: Stay informed about market trends, economic indicators, and other factors that could impact options prices. Continuously educate yourself about advanced options trading strategies and risk management techniques.
By implementing these risk management strategies, you can minimise your downside risk while maximising your potential returns in advanced options trading.
Last, but not least, we will see the resources available for learning options trading.
Resources to learn options trading
Learners who are aware of options trading and implementing options trading strategies can start by expanding their knowledge with this list of reads and projects on options trading.
- Exotic Options
- Swaption
- Dispersion Trading
- What are leaps - Leap options and leap option strategy
- Machine Learning options trading
- Index Options Project
- Dispersion Trading Project
- Index Arbitrage
We have curated a list of some of our most demanded blogs on Options Trading written by experts! Do check them out!
Frequently asked questions on advanced options trading
Below are the questions that options traders usually ask. So, we have provided the answer to each ahead.
Q: What are the main factors influencing options pricing in advanced trading?
A: Options pricing in advanced trading is influenced by several factors:
- Underlying Asset Price: The current price of the underlying asset significantly affects the option's value.
- Strike Price: The relationship between the strike price and the current price of the underlying asset impacts the option's intrinsic value.
- Time to Expiry: The amount of time remaining until the option expires affects its time value.
- Volatility: Implied volatility measures the market's expectation of future volatility and has a significant impact on options pricing.
- Interest Rates: Changes in interest rates can affect the present value of the option's cash flows.
- Dividends: For options on stocks, the timing and size of dividend payments can affect options pricing.
Q: How do I choose the right options contract for advanced trading?
A: Choosing the right options contract involves considering several factors:
- Underlying Asset: Select options contracts based on underlying assets with which you are familiar and have thoroughly analysed.
- Market Conditions: Consider the current market conditions, including volatility, trend, and liquidity.
- Trading Objectives: Determine your trading objectives, whether you're looking for income generation, speculation, or hedging.
- Risk Tolerance: Assess your risk tolerance and choose options contracts that align with your risk management strategy.
- Options Greeks: Analyse options Greeks to understand the sensitivity of options prices to changes in various factors.
- Expiration Date: Choose an expiration date that aligns with your trading timeframe and expectations for the underlying asset.
Q: What role does implied volatility play in advanced options trading?
A: Implied volatility is a critical factor in options pricing and advanced options trading:
- Options Pricing: Implied volatility reflects the market's expectations for future volatility and is a key input in options pricing models.
- Strategy Selection: High implied volatility may lead to overpriced options, making strategies like selling options more attractive, while low implied volatility may favour buying options.
- Risk Management: Implied volatility can help traders assess the potential risk of their options positions and adjust their strategies accordingly.
- Market Sentiment: Changes in implied volatility can indicate shifts in market sentiment and provide insights into future price movements.
Q: What are some common mistakes to avoid in advanced options trading?
A: Common mistakes to avoid in advanced options trading include:
- Over leveraging: Trading with excessively large positions relative to account size.
- Ignoring Risk Management: Failing to use stop-loss orders or risk management techniques to limit losses.
- Neglecting Implied Volatility: Not considering implied volatility when selecting options strategies.
- Lack of Diversification: Concentrating trades in a single underlying asset or strategy, increasing portfolio risk.
- Chasing Returns: Focusing solely on potential profits without considering potential risks.
- Failing to Plan: Trading without a well-defined trading plan or strategy.
- Ignoring Market Conditions: Failing to adapt trading strategies to current market conditions.
Q: How do I stay updated on market developments relevant to advanced options trading?
A: You can stay updated on market developments by:
- Market Research: Regularly review financial news, market analysis, and economic reports to stay informed about developments that may impact options prices.
- Technical Analysis: Monitor technical indicators and chart patterns to identify potential trading opportunities.
- Options Education: Continuously educate yourself about advanced options trading strategies and risk management techniques.
- Professional Analysis: Follow market analysts, traders, and financial experts who provide insights and analysis relevant to options trading.
- Online Communities: Join online forums, trading communities, and social media groups to discuss trading ideas and stay updated on market trends.
- Broker Tools: Utilise research tools and resources provided by your broker, such as market scanners, options screeners, and research reports.
Q: Can I use advanced options trading strategies in different market conditions?
A: Yes, advanced options trading strategies can be used in various market conditions:
- Bullish Markets: Strategies like long calls, short puts, bull call spreads, and covered calls can be used in bullish markets to profit from upward price movements.
- Bearish Markets: Strategies like long puts, short calls, bear put spreads, and bear call spreads can be used in bearish markets to profit from downward price movements.
- Sideways Markets: Strategies like iron condors, butterflies, and calendar spreads can be used in sideways markets to profit from range-bound price movements.
- High Volatility Markets: Strategies like straddles, strangles, and ratio spreads can be used in high volatility markets to profit from large price movements or changes in implied volatility.
Conclusion
Advanced options trading offers a vast array of strategies and tools for investors looking to manage risk effectively. Understanding options Greeks, that is, Delta, Gamma, Vega, and Theta is crucial, as they directly impact options pricing and portfolio management.
Volatility strategies are quite essential for success in advanced options trading, and mastering the skills required for implementing these strategies is key.
Knowing how options are priced, the factors influencing pricing, and the various options pricing models are fundamental. Risk management is paramount, and learning how to effectively analyse options Greeks and avoid common mistakes is essential for success. Staying updated on market developments and utilising available resources, such as advanced options trading courses and books, is vital for continuous learning and improvement.
By following the right approach and utilising the right broker, traders can navigate the world of advanced options trading with confidence and competence.
To learn more about advanced options trading, our learning track on Quantitative Trading in Futures and Options Markets covers a bundle of 7 courses to start using quantitative techniques in futures & options trading. With these courses, you will learn volatility forecasting, options backtesting, risk management, option pricing models, greeks, and various strategies such as straddle, butterfly, iron condor, spread strategies, dispersion trading, sentiment trading, box strategy, diversified futures trading strategies and much more.
Files in the download:
- Put call parity - Python notebook
- Butterfly strategy - Python notebook
Author: Chainika Thakar and Rekhit Pachanekar
Disclaimer: All investments and trading in the stock market involve risk. Any decision to place trades in the financial markets, including trading in stock or options or other financial instruments is a personal decision that should only be made after thorough research, including a personal risk and financial assessment and the engagement of professional assistance to the extent you believe necessary. The trading strategies or related information mentioned in this article is for informational purposes only.

