By Rekhit Pachanekar and Chainika Thakar
If you think investing in options is just another way to make money and was created by some fancy guys in suits working at Wall Street, you are wrong. The options world predates the modern stock exchanges by a large margin.
Some credit the Samurai for giving us the foundation on which options contracts were based. While some others acknowledge the Greeks for providing us with an idea of how to speculate on a commodity; in this case, the harvest of olives.
In both cases, humans were trying to guess the price of a food item and trade accordingly (rice in the case of samurais), long before the modern world put in various rules and set up exchanges.
- What is options trading?
- Common terms used in options trading
- Example
- Types of options
- Visualise options profit and loss
- Options payoff diagram
- Options trading vs stock trading
What is options trading?
Before we get started, to learn about options trading, let’s take a moment to understand what options trading is and why we need options at all.
Let’s take a very simple example to understand options trading.
Consider that you are buying a stock for Rs. 3000. But the broker tells you about an exciting offer, that you can buy it now for Rs. 3000 or you can give a token amount of Rs. 30 and reserve the right to buy it at Rs. 3000 after a month, even if the stock increases in value at that time. But that token amount is non-refundable!
You realise that there is a high chance that the stock would cross Rs. 3030, thus, you can break even at least. Since you have to pay only Rs. 30 now, the remaining amount can be used elsewhere for a month. You wait for a month and then look at the stock price.
Now, depending on the stock price, you have the option to buy the stock from the broker or not. Of course, this is an over-simplification, but this is options trading in a gist.
In the world of trading, options are instruments that belong to the derivatives family, which means their price is derived from something else, mostly stocks. The price of an option is intrinsically linked to the price of the underlying stock.
Common terms used in options trading
In the case of options trading, we use certain terms to create a successful strategy. Let us learn about these common terminologies while trading with options. These terms are:
- Call
- Put
- Strike price
- Premium
- Underlying asset
- Expiration date
- Options style
- Moneyness
Call
A call option is an option contract that gives the buyer of the contract the right, but not the obligation, to purchase the underlying security at the strike price on or before (depending on option type) the expiration date. The seller, or writer, of the call option has an obligation to sell the underlying should the buyer of the contract choose to exercise his/her right to purchase the underlying.
Put
Put option is a derivative instrument which gives the buyer of the option (holder) the right but not the obligation to sell the underlying asset at a fixed price (exercise or strike price) after a specified period of time (on maturity for European and anytime before maturity for American option).
The seller of the put option (put writer) has a contingent obligation to purchase the underlying asset if the put holder wishes to exercise the option. As the option gives the buyer a choice to exercise the option or not, the seller charges a fixed upfront fee from the buyer (known as a premium).
Strike Price
The strike price is the price at which the underlying stocks can be bought or sold as per the contract. In options trading, the strike price for a call option indicates the price at which the stock can be bought on or before its expiration. For put options trading, stock price refers to the price at which the seller of the underlying can exercise its right to sell the underlying stocks (on or before its expiration).
Premium
Since the options themselves don’t have an underlying value, the options premium is the price you have to pay to purchase an option. The premium is determined by multiple factors, including the underlying stock price, volatility in the market and the days until the option’s expiration. In options trading, choosing the premium is one of the most essential components.
Underlying Asset
In options trading, the underlying asset can be stocks, futures, index, commodities or currency. The price of options is derived from its underlying asset. For the purpose of this article, we will be considering the underlying asset as the stock. The option of stock gives the right to buy or sell the stock at a specific price and date to the holder.
Expiration Date
In options trading, all stock options have an expiration date. The expiration date is also the last date on which the holder of the option can exercise the right to buy or sell the options that are in holding. In options Trading, the expiration of options can vary from weeks to months to years, depending upon the market and the regulations.
Options Style
There are two major types of options that are practised in most options trading markets.
- American Options, which can be exercised anytime before their expiration date
- European Options, which can only be exercised on the day of their expiration
Moneyness (ITM, OTM & ATM)
It is very important to understand the options moneyness before you start trading in Stock options. A lot of options trading strategies are played around the moneyness of an option.
It basically defines the relationship between the strike price of an option and the current price of the underlying stock. We will discuss each term briefly below.
When is an Option in-the-money?
- Call Option - when the underlying stock price is higher than the strike price
- Put Option - when the underlying stock price is lower than the strike price
When is an Option out-of-the-money?
- Call Option - when the underlying stock price is lower than the strike price
- Put Option - when the underlying stock price is higher than the strike price
When is an Option at-the-money?
- When the underlying stock price is equal to the strike price.
Take a break here to ponder over the different terms, as we will find it extremely useful later when we go through the types of options as well as a few options trading strategies.
Example
Let us go through two examples to better understand the call and put options and the strategy built based on both.
For simplicity’s sake, let us assume the following:
- Price of Stock when the option is written: $100
- Premium: $5
- Expiration date: 1 month after the option is bought
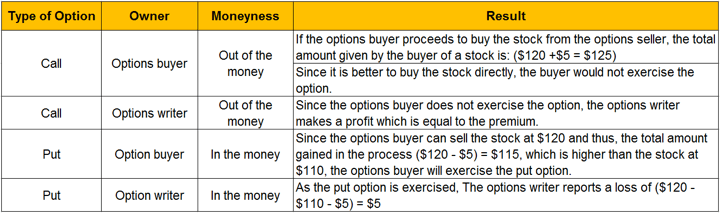
Case 1:
The current price of stock: $110. Strike price: $120
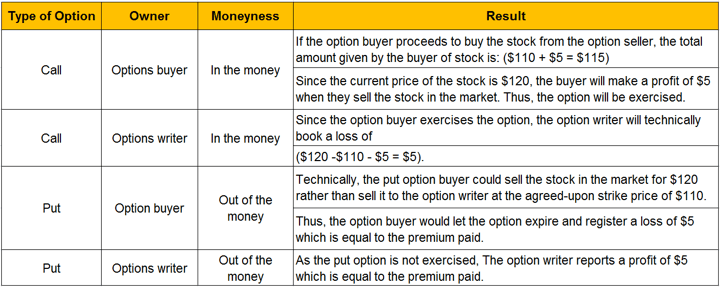
Case 2:
The current price of stock: $120. Strike price: $110
Supercharge Your Options Trading with Machine Learning! Watch this mind-blowing video on and discover how cutting-edge technology is revolutionizing the trading strategies. Elevate your trading skills to new heights with this game-changing opportunity!
Types of options
In the true sense, there are only two types of options, i.e call & put options. We will understand them in more detail so as to learn about options trading in depth. Learn Machine Learning for Options Trading in detail in the Quantra course.
Put-call options from the buyers' point of view
In order for you to make a profit, the price of the stock should go down from the strike price plus the premium of the put option that you have purchased before or at the time of its expiration. Similarly, for making a profit with the call option, the price of the underlying stock should be higher than the strike price plus the premium of the call option that you have bought before or at the time of the expiration.
In this manner, both put and call option buyer’s loss is limited to the premium paid but the profit is unlimited. The above explanations were from the buyer's point of view.
Put-call options from the sellers' point of view
We will now understand the put-call options from the seller’s point of view, i.e., options writers. The Put option seller, in return for the premium charged, is obligated to buy the underlying asset at the strike price.
Similarly, in return for the premium charged, the call option seller is obligated to sell the underlying asset at the strike price.
Visualise options profit and loss
Now, is there a way to visualise the potential profit/loss of an option buyer or seller? Actually, there is!
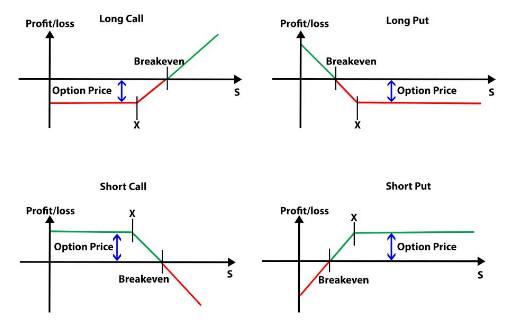
An option payoff diagram is a graphical representation of the net Profit/Loss made by the option buyers and sellers.
Before we go through the representation of each in the diagram, let’s understand what the four terms mean. As we know that going short means selling and going long means buying the asset, the same principle applies to options.
Keeping this in mind, we will go through the following four terms.
- Short call - Here, we are betting that the prices will fall and hence, a short call means you are selling calls.
- Short put - Here, the short put means we are selling a put option
- Long call - it means that we are buying a call option since we are optimistic about the underlying asset’s share price
- Long put - Here, we are buying a put option.
Options payoff diagram
Going forward, we will now discuss the options payoff diagram below.
where,
S = Underlying Price
X = Strike Price
Break-even point is that point at which you make no profit or loss.
The long call holder makes a profit equal to the stock price at expiration minus strike price minus premium if the option is in the money. The call option holder makes a loss equal to the premium amount if the option expires out of money and the writer of the option makes a flat profit equal to the option premium.
Similarly, profit is made for the put option buyer when the option is in the money and is equal to the strike price minus the stock price at expiration minus the premium. And the put writer makes a profit equal to the premium for the option.
Options trading vs stock trading
There must be doubt in your mind about why we even have options trading if it is just another way of trading. Well, here are a few points which make it different from trading stocks:
- The options contract has an expiration date, unlike stocks. The expiration can vary from weeks to months to years depending upon the regulations and the type of options that you are practising. Stocks, on the other hand, do not have an expiration date.
- Unlike Stocks, Options derive their value from something else, and that’s why they fall under the derivatives category
- Options are not definite by numbers like stocks
- Options owners have no right (voting or dividend) in a company unlike stock owners
It is quite often that some people find the option’s concept difficult to understand though they have already followed it in their other transactions, for e.g. car insurance or mortgages. In this part of the article, we will take you through some of the most important advanced options trading aspects before we get down to the world of options trading.
Lat but not the least, you can through our curated list of some of our most demanded blogs on options trading written by experts! This way you can navigate your way through the basic to advanced topics to bring you the knowledge needed for options trading starting from the basics.
Conclusion
We have covered all the basics of options trading which include the different Option terminologies as well as types. We also went through an example meant for options trading beginners and option greeks. We understood various options trading strategies and things to consider before opening an options trading account.
If you're interested in the basics of options trading, this blog would be the perfect starting point. However, if you wish to continue learning by yourself, our free options trading course is what you need. It starts with basic terminology and concepts you must know to be able to trade Options.
The world of options trading isn't limited to this. To go ahead, one needs to start using quantitative techniques in options & futures trading system and learn to create option pricing models, option greeks and various strategies. With our learning track, it is possible to develop a quantitative approach in Futures & Options Trading.
Disclaimer: All data and information provided in this article are for informational purposes only. QuantInsti® makes no representations as to accuracy, completeness, currentness, suitability, or validity of any information in this article and will not be liable for any errors, omissions, or delays in this information or any losses, injuries, or damages arising from its display or use. All information is provided on an as-is basis.


