Recursive Functions in Python: Concepts, Types, and Applications in Trading

By Chainika Thakar (Originally written by Prachi Joshi )
Recursive functions in Python are valuable for solving complex problems by calling themselves during execution and by breaking problems into smaller parts. In this blog, we will explore different types of recursive functions, their construction, and their problem-solving benefits. Efficient recursive functions are crucial in trading for performance and memory management.

We will examine their applications in trading, such as market data analysis and risk management, while addressing challenges like memory usage and debugging. Advanced topics like tail recursion and nested recursion will also be briefly covered. This knowledge enables traders to develop advanced strategies, enhance performance, and manage market complexities.

As Ken Thompson once said:

“One of my most productive days was throwing away 1000 lines of code.”

This is partially achievable with the help of “Recursive Functions in Python”!
Let us find out how with this blog that covers:

What is a recursive function in Python?
Example of recursive function in Python
Types of recursive functions in Python
Advanced topics in recursion
How to call a recursive function?
Recursive functions vs. iterative functions in Python
How to write efficient recursive functions?
Applications of recursive functions in trading
Applications of recursive functions with Python for trading
Misconceptions with recursive functions in Python
Advantages of recursive function
Disadvantages of recursive function

What is a recursive function in Python?

A recursive function in Python programming is a function that calls itself during its execution. This allows the function to repeat itself until it reaches a base case, which is a condition that stops the recursion. Recursive functions are often used to solve problems that can be broken down into smaller, similar subproblems.

Next, let us see an example of recursive functions in Python to learn about them in detail.

Example of recursive function in Python

Here is a simple example to illustrate a recursive function:

Output:
120

In this example, the factorial function calculates the factorial of a non-negative integer n. The base case is when n is 0, which returns 1. For other values of n, the function calls itself with n-1 and multiplies the result by n, thus building up the factorial value through recursive calls. ⁽¹⁾

Now we can move to the types of recursive functions in Python to learn how each type works.

Types of recursive functions in Python

In Python, recursive functions can be categorised into different types based on their structure and how they make recursive calls.⁽²⁾

The main types are:

Direct Recursion

A function directly calls itself within its own body.

Example:

Output:
120

Indirect Recursion

A function calls another function which, in turn, calls the first function creating a cycle.

Example:

Output:
3
2
1

Let us now check the advanced topics in recursion.

Advanced topics in recursion

The two advanced topics in recursion are -

Types of advanced recursive functions in Python

Tail Recursion

Tail recursion occurs when the recursive call is the last operation performed by the function before returning a result. In other words, the recursive call is in the tail position, and there are no further operations to perform after the recursive call returns.

Tail recursion is significant because it allows some programming languages to optimise recursive calls, known as tail call optimisation (TCO). In languages that support TCO, like Scheme or some functional programming languages, tail-recursive functions can execute with constant stack space, avoiding the risk of stack overflow. However, it is essential to note that Python does not perform automatic tail call optimisation.

Nested Recursion

Nested recursion refers to a scenario where a recursive function calls itself with a parameter that is the result of another recursive call. In other words, the function's parameter includes a recursive call within its expression. This recursive call can occur within the function's arguments or within the function's return statement.

Nested recursion can result in a more complex recursive process where each level of recursion contains its own set of recursive calls. Understanding and managing nested recursion can be challenging due to its nested nature and the potential for multiple levels of recursion.

Moving forward, we will discuss how to call a recursive function to make it useful.

How to call a recursive function?

Below are the steps to call a recursive function.

Steps to call a recursive function in Python

Step 1: Define the function with a clear base case and a recursive case. Write the function including a base case to end the recursion and a recursive case to continue the process.
Step 2: Call the function with the initial arguments. Invoke the recursive function with the starting values for its parameters.
Step 3: The function calls itself with modified arguments, progressing towards the base case. The function repeatedly invokes itself with updated parameters that move closer to the base case.
Step 4: When the base case is met, the function stops calling itself. Upon reaching the base case, the function ceases further recursive calls and begins returning results.

Now we will find out the difference between recursive functions and iterative functions in Python.

Recursive functions vs. iterative functions in Python

Below you will see the difference between recursive and iterative functions in Python with each aspect classifying the difference and making it clearer to understand. ⁽³⁾

Aspect	Recursive Functions	Iterative Functions
Definition	A function that calls itself to solve a problem.	A function that uses loops to repeat a set of instructions until a condition is met.
Advantages	Simplicity and clarity for naturally recursive problems. A natural fit for problems that break down into smaller subproblems. Leads to more concise and readable code.	Efficiency in memory and speed. No risk of stack overflow. Predictable performance and easier to optimise.
Disadvantages	Risk of stack overflow with deep recursion. Performance overhead due to function call management. Higher memory usage due to additional stack frames.	Can be more complex and harder to understand for naturally recursive problems. May require more boilerplate code for managing loops and state.
Example	def factorial_recursive(n): if n == 0: return 1 else: return n * factorial_recursive(n - 1) print(factorial_recursive(5)) Output: 120	def factorial_iterative(n): result = 1 for i in range(1, n + 1): result *= i return result print(factorial_iterative(5)) Output: 120
When to Use	When the problem is naturally recursive (e.g., tree/graph traversal, combinatorial problems). When the recursive solution is significantly simpler and more readable. When the problem size is small enough to avoid stack overflow issues.	When performance and memory usage are critical. When the problem can be easily and straightforwardly solved with loops. When dealing with large input sizes where recursion depth could be problematic.

Next, we can find out how to write efficient recursive functions.

How to write efficient recursive functions?

Writing efficient recursive functions involves optimising both the algorithmic approach and the implementation details. ⁽⁴⁾

Here are some tips for writing efficient recursive functions in Python:

Write efficient recursive functions in Python

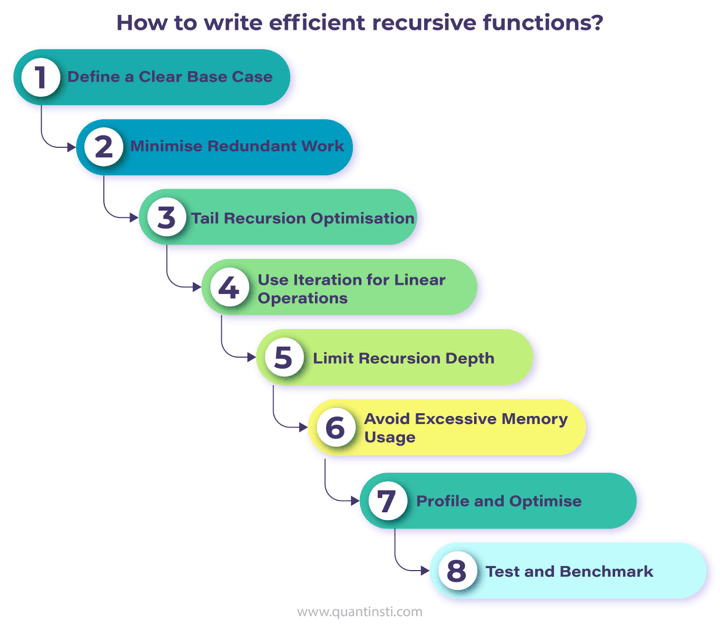
Define a Clear Base Case: Ensure that your recursive function has a clear base case that terminates the recursion. This prevents unnecessary recursive calls and ensures that the function doesn't run indefinitely.
Minimise Redundant Work: Avoid performing redundant computations by caching or memorising intermediate results when appropriate. This can significantly reduce the number of recursive calls and improve performance.
Tail Recursion Optimisation: Whenever possible, try to structure your recursive function so that the recursive call is the last operation performed before returning a result. This allows for tail call optimisation, which eliminates the need to maintain a call stack and can reduce memory usage.
Use Iteration for Linear Operations: For tasks that involve linear operations (such as traversing arrays or lists), consider using iteration instead of recursion. Iterative solutions often have better performance characteristics and are less likely to encounter stack overflow errors.
Limit Recursion Depth: If your recursive function has the potential to recurse deeply, consider implementing a depth limit or using an iterative approach for large inputs to avoid stack overflow errors.
Avoid Excessive Memory Usage: Be mindful of memory usage when working with recursive functions, especially for problems with large input sizes. Use data structures efficiently and avoid unnecessary memory allocations.
Profile and Optimise: Profile your recursive function to identify performance bottlenecks and areas for optimisation. Consider alternative algorithms or data structures if necessary to improve efficiency.
Test and Benchmark: Test your recursive function with various input sizes and scenarios to ensure it performs efficiently across different use cases. Benchmark your implementation against alternative solutions to validate its efficiency.

By following these tips and considering the specific characteristics of your problem, you can write efficient recursive functions that balance performance with readability and maintainability.

There are certain use cases of recursive functions in Python which we will discuss as we move to the next section.

Applications of recursive functions in trading

Recursive functions can be utilised in various aspects of trading in Python, including data analysis, strategy implementation, and risk management. Here are some potential use cases of recursive functions in trading:

Technical Indicator Calculations

Recursive functions can be used to calculate various technical indicators such as moving averages, exponential moving averages, and stochastic oscillators. For example, as a technical indicator-based strategy, a recursive function can calculate the moving average of a stock price by recursively updating the average with new data points.

If you wish to know about some technical indicators strategies with Python, they are in this video below:

Backtesting Strategies

Recursive functions are useful for backtesting trading strategies that involve iterating over historical data. For instance, a recursive function can simulate the execution of buy and sell signals over a historical price dataset to evaluate the performance of a trading strategy.

Risk Management

Recursive functions can aid in risk management by recursively calculating position sizes based on portfolio value, risk tolerance, and stop-loss levels. This helps traders determine the appropriate position size to limit potential losses while increasing growth opportunities.

Portfolio Optimisation

Recursive functions can be applied in portfolio optimisation algorithms that recursively iterate over different asset allocations to minimise risk. This involves recursively evaluating the performance of each portfolio allocation based on historical data for constructive portfolio management.

Portfolio and risk management can be organised and implemented in the way mentioned in the video for increasing the chances of growth in your trades.

Option Pricing Models

Recursive functions play a crucial role in option pricing models such as the binomial option pricing model and the Cox-Ross-Rubinstein model. These models recursively calculate the option price at each node of a binomial tree to determine the fair value of an option. These pricing models are imperative concepts of options trading strategies.

The option pricing can be made subtle if right practices are in place which are mentioned in this video.

Now, we will discuss the applications of recursive functions in trading using Python.

Applications of recursive functions with Python for trading

In trading, recursive functions can be utilised for various purposes, such as calculating financial indicators, analysing stock price patterns, and making trading decisions.

Below is the example of recursive functions in Python for trading applications.

Example: Calculating Fibonacci Retracement Levels

Fibonacci retracement levels are popular among traders for identifying potential support and resistance levels and are a part of the price action trading strategy. These levels are based on the Fibonacci sequence, which can be calculated using a recursive function.

Output:

Fibonacci Levels     Retracement Levels  
0                    100.0               
1                    98.52941176470588   
1                    98.52941176470588   
2                    97.05882352941177   
3                    95.58823529411765   
5                    92.6470588235294    
8                    88.23529411764706   
13                   80.88235294117646   
21                   69.11764705882354   
34                   50.0                
High                 100                 
Low                  50

Here is what is happening in the code above:

The Fibonacci function calculates the Fibonacci number at position n recursively.
We calculate the first 10 Fibonacci levels and store them in the fib_levels list.
The retracement_levels function computes the Fibonacci retracement levels based on a given high and low price.
The retracement levels are derived by applying the Fibonacci ratios to the price range between the high and low prices.

The output is as follows:

Fibonacci Levels:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34: The first 10 Fibonacci numbers.
Retracement Levels: Calculated from a high price of 100 and a low price of 50, these levels represent the price points where the stock might find support or resistance.
Detailed Significance of Each Pair:
0 - 100.0: The highest price level (0th Fibonacci number maps to the high price).
1 - 100.0: The 1st Fibonacci number maps to 100.0 (high price).
1 - 90.0: The 2nd Fibonacci number maps to 90.0.
2 - 80.0: The 3rd Fibonacci number maps to 80.0.
3 - 70.0: The 4th Fibonacci number maps to 70.0.
5 - 60.0: The 5th Fibonacci number maps to 60.0.
8 - 50.0: The 6th Fibonacci number maps to 50.0 (low price).
13 - 43.333333333333336: The 7th Fibonacci number maps to 43.33.
21 - 36.666666666666664: The 8th Fibonacci number maps to 36.67.
34 - 30.0: The 9th Fibonacci number maps to 30.0.
High and Low Levels:
High - 100.0: Explicitly shows the high price.
Low - 50.0: Explicitly shows the low price.
Practical use in trading

Traders use these retracement levels to identify potential areas where the price might reverse or continue its trend. As shown in the example above, if the price is retracing back to 70.0 (which corresponds to the 3rd Fibonacci number), traders might look for a reversal signal at this level.

Now let us talk about the misconceptions while working with the recursive functions in Python which must be avoided.

Misconceptions with recursive functions in Python

Misconceptions about recursive functions in Python can lead to confusion and errors in code. Here are some common misconceptions to be aware of:

Recursion is Always Better than Iteration: While recursion can be an elegant solution for certain problems, it is not always the most efficient or practical choice. Sometimes, iterative solutions may offer better performance, readability, and simplicity.
Recursion is Only for Mathematical Problems: While recursion is commonly associated with mathematical problems like factorial calculation or Fibonacci sequence generation, it can be applied to various other domains, including data structures, algorithms, and problem-solving.
All Recursive Functions are Tail-Recursive: Not all recursive functions are tail-recursive, where the recursive call is the last operation performed. Tail recursion allows for optimisation in some programming languages, but Python does not optimise tail calls by default.
Recursion Always Leads to Stack Overflow: While recursive functions can potentially lead to stack overflow errors if the recursion depth is too deep, this is not always the case. Properly designed recursive functions with appropriate termination conditions and limited recursion depth can avoid stack overflow.
Recursive Functions are Always Hard to Debug: While recursive functions can be challenging to debug due to their recursive nature, proper testing, logging, and debugging techniques can help identify and resolve issues effectively. Understanding the flow of recursive calls and using tools like print statements or debuggers can simplify debugging.
Recursion is Always Slower than Iteration: Recursive functions may incur overhead due to function calls and stack management, but this does not necessarily mean they are always slower than iterative solutions. Depending on the problem and implementation, recursive functions can be just as efficient as iterative counterparts.
Recursion Always Requires More Memory: While recursive functions may consume additional memory due to the call stack, this does not necessarily mean they always require more memory than iterative solutions. Properly optimised recursive functions can minimise memory usage and perform efficiently.
Recursion is Always the Most Readable Solution: While recursion can lead to elegant and concise code for certain problems, it may not always be the most readable solution, especially for developers unfamiliar with recursive techniques. Choosing the most readable solution depends on the problem domain and the audience.

Going forward, there are several advantages of recursive functions that we will look at.

Advantages of recursive function

Here are some advantages of using recursive functions:

Simplicity and Clarity: Recursive solutions often provide a clearer and more intuitive way to express algorithms, especially for problems with a natural recursive structure. This can lead to code that is easier to understand and maintain.
Natural Fit for Certain Problems: Problems that can be divided into smaller subproblems, such as tree traversal, pathfinding, or sorting algorithms like quicksort and mergesort, lend themselves well to recursive solutions.
Code Conciseness: Recursive functions can often lead to more concise and readable code compared to equivalent iterative solutions. This can result in simpler and more elegant implementations of algorithms.
Problem Decomposition: Recursive functions facilitate problem decomposition by breaking down complex problems into smaller, more manageable subproblems. Each recursive call focuses on solving a smaller instance of the problem, leading to modular and reusable code.
Dynamic Problem Solving: Recursive functions allow for dynamic problem solving, where the size of the problem can vary at runtime. This flexibility makes recursive solutions suitable for problems with variable input sizes or unknown depths.
Ease of Implementation: In many cases, implementing a recursive solution is more straightforward and requires fewer lines of code compared to iterative approaches. This simplicity can lead to faster development and easier prototyping.

Overall, recursive functions offer several advantages, including simplicity, clarity, conciseness, problem decomposition, dynamic problem solving, and ease of implementation. These benefits make recursive programming a valuable tool for solving a wide range of problems in Python and other programming languages.

Not only advantages, but there are several disadvantages also of the recursive function. Let us discuss the same.

Disadvantages of recursive function

While recursive functions can be useful in certain aspects of trading, such as data analysis or strategy development, they also come with disadvantages when applied in trading scenarios:

Risk of Stack Overflow: Recursive functions can potentially lead to stack overflow errors, especially when dealing with large datasets or deep recursion. In trading applications, where processing extensive historical data or complex algorithms is common, stack overflow errors can occur if the recursion depth exceeds system limits.
Performance Overhead: Recursive calls involve overhead due to function call management, which can impact the performance of trading systems, especially in real-time or high-frequency trading environments. The additional memory allocation and stack frame management can introduce latency, affecting the responsiveness of the trading system.
Memory Usage: Recursive functions can consume more memory than iterative solutions, particularly when dealing with deep recursion or large datasets. In trading applications where memory resources may be limited, excessive memory usage by recursive functions can be problematic and lead to performance degradation.
Difficulty in Debugging: Debugging recursive functions in trading applications can be challenging due to their recursive nature and potential for multiple recursive calls. Understanding the flow of execution, tracking variables, and identifying errors across recursive calls can complicate the debugging process, leading to longer development cycles and potential errors in trading algorithms.
Complexity of Algorithm Design: Designing and implementing recursive algorithms for trading strategies or risk management systems can be complex, especially for traders or developers with limited experience in recursive programming. Recursive solutions may introduce additional complexity and require a deeper understanding of algorithmic principles.
Maintainability and Scalability: Recursive functions may not always be the most maintainable or scalable solution for trading systems, especially as the complexity and size of the codebase grow. Recursive algorithms can be harder to maintain, modify, and optimise compared to iterative solutions,x making them less suitable for large-scale trading applications.
Lack of Tail Call Optimisation (in Python): Python does not perform automatic tail call optimisation, limiting the optimisation benefits of tail recursion in trading applications. This means that recursive functions in Python may still incur stack overhead, even if they are tail-recursive, potentially impacting the performance of trading algorithms.

Conclusion

In conclusion, recursive functions in Python offer a powerful and elegant approach to problem-solving, particularly in trading applications. Despite their advantages, such as simplicity, modularity, and dynamic problem-solving, recursive functions come with challenges, including the risk of stack overflow and debugging complexities.

However, by understanding their nuances and applying efficient coding practices, traders can harness the full potential of recursive functions to develop robust trading algorithms, optimise performance, and mitigate risks effectively. Moreover, the advanced topics like tail recursion and nested recursion which were covered in brief, provide further insights into their functionalities and optimisation techniques.

With this knowledge, traders can navigate the dynamic landscape of financial markets, leveraging recursive functions as indispensable tools in their quest for trading success.

To increase your knowledge of Python, you can explore more with the course Python for Trading which is an essential course for quants and finance-technology enthusiasts. With this course, you can get started in Python programming and learn to use it in financial markets. It covers Python data structures, Python for data analysis, dealing with financial data using Python, and generating trading signals among other topics.

Note: The original post has been revamped on 27^th June 2024 for recentness, and accuracy.

Disclaimer: All data and information provided in this article are for informational purposes only. QuantInsti® makes no representations as to accuracy, completeness, currentness, suitability, or validity of any information in this article and will not be liable for any errors, omissions, or delays in this information or any losses, injuries, or damages arising from its display or use. All information is provided on an as-is basis..

Live Q&A | Skills to Get Quant Jobs